Matriks dan sistem persamaan
A.
Sistem Persamaan Linier
1. Sistem Persamaan Linier
Suatu
persamaan linier dalam n peubah (variabel) adalah persamaan dengan bentuk:
a1x1
+ a2x2 + . . . anxn = b
dimana a1, a2 . . . andan b adalah bilangan-bilangan
real dan x1, x2 .
. . x adalah peubah. Dengan demikian maka suatu sistem linier dari m persamaan dalam
n peubah adalah suatu sistem yang berbentuk :
a11x1+
a12x2 + . . . anxn= b1
a21x1+ a2x2
+ . . . a2nxn = b2
.
.
am1x1 + am2x2
+ . . . amnxn =bm
dimana aijdan bi semuanya adalah bilangan
real. Kita akan meyenbut sistem-sistem bentuk 1 sebagai sistem linier m x n
contohnya ialah :
a.
x1 + 2x2 = 5 b. x1 – x2
+ x3 = 2 c.
x1 + x2 = 2
2x1 + 3x2 = 8 2x1 + x2 + x3 = 4 x1 – x2 = 1
x1 = 4
Sistem
(a) adalah sistem 2 x 2, (b) adalah sistem 2x3, dan (c) adalah sistem 3x2.
Yang
dimaksud dengan penyelesaian sistem m x n) adalah tupel-n terurut bilangan-bilangan
(x1, x2, . . .,xn) yang memenuhi semua persamaan
dalam sistem. Sebagai contoh pasangan terurut (1, 2) adalah penyelesaian dari sistem
(a), karena:
1
.(1) + 2. (2) = 5
2. (1) + 3.(2)
= 8
Tupel terurut (2,0,0) adalah penyelesaian
dari sistem (b) karena:
1 . (2) – 1. (0)
+ 1. (0) = 2
2. (2) +
1. (0) – 1 . (0) = 4
Sebenarnya
sistem (b) memiliki banyak penyelesaian. Jika a
adalah sembarang bilangan real, maka dapat dilihat dengan mudah bahwa tupel
berturut-turut (2, a, a)
dalah suatu penyelesaian. Akan tetapi sistem (c) tidak memilki penyelesaian.
Terlihat dari persamaan ketiga bahwa koordinat pertama dari sembarang
penyelsaian harus memilki nilai 4. Dengan menggunakan x1 = 4 dalam
kedua penyelesaian yang pertama. Jika dilihat lagi bahwa koordinat kedua harus
memenuhi :
4
+ x2 = 2
4
– x2 = 1
Karena
tidak terdapat bilangan real yang memenuhi kedua persamaan ini, maka sistem (c)
tidak memiliki penyelesaian. Jika linier tidak memiliki penyelesaian, maka dikatakan
sistem tersebut adalah tak konsisten (inconsistent).
Jika sistem linier mempunyai paling sedikit satu penyelesaian, dikatakan sistem
tersebut konsisten (consistent).
2. Sistem
Ekivalen
Tinjau
dua sistem:
(a) 3x1
+ 2x2 – x3 = -2 (b) 3x1 + 2x2 – x3 = -2
x2 = 3 -3x1 – x2 + x3 = 5
2x3 =
4 3x1 + 2x2 + x3 = 2
Sistem
(a) mudah diselesaikan, karena x2 = 3 dan x3= 2. Dengan menggunakan
kedua nilai ini akan diperoleh:
3x1+
2.3 – 2 = - 2
x1 = - 2
jadi penyelesaian dari sistem (a)
adalah ( -2, 3, 2). Sistem (b) tampaknya lebih sulit untukdiselesaikan,
penyelesaian sistem (b) sebagai berikut:
3x1+ 2x2 – x3 = -2
-3x1 – x2 + x3 =
5
x2 = 3
Jika
(x1 , x2 , x3 ) adalah sembarang penyelesaian
(b), maka (x1 , x2 , x3 ) harus memenuhi semua
persamaan dari sistem. Maka penyelesaian berikutnya:
3x1+ 2x2 + x3 = 2
3x1 + 2 x2 – x3 = -2
2x3 = 4
Dengan
metode subtitusi diperoleh tupel terurut (-2, 3, 2), sehingga mempunyai himpunan
penyelesaian yang sama dengan sistem (a).
Berikut
adalah tiga operasi yang dapat digunakan pada suatu sistem untuk memperoleh
sistem yang ekivalen :
I.
Urutan penulisan dua persamaan dapat
dipertukarkan
II.
Kedua ruas dari suatu persamaan
dapat dikalikan dengan bilangan real bukan nol yang sama.
III.
Kelipatan dari suatu persamaan dapat
dijumlahkan pada persamaan yang lain.
3. Sistem n x n
Suatu sistem dikatakan memiliki bentuk segitiga,
jika koefisien-koefisien dari k-1 peubah yang pertama dalam persamaan ke- k semuanya
nol dan koefisien dari xk adalah bukan nol (k =1, …,n).
Contoh:
3x1+ 2x2 + x3 = 1
x2 + x3 =
2
2 x3 =
4
Memiliki
bentuk segitiga, karena koefisien-koefisien dalam persamaan kedua masing-masing
adalah 0, 1, -1, dan koefisien-koefisien dalam persamaan ketiga masing-masing adalah
0,0,2. Karena bentuk segitiga, persamaan ini mudah diselesaikan.
Metode
yang digunakan dalam persamaaan ini adalah Back substitution atau subtitusi
balik. Pertama, persamaan ke-n diselesaikan untuk mendapatkan nilai xn.
Nilai ini digunakan dalam persamaan ke n-1 untuk mendapatkan nilai x n-1 dan
nilai xndan x n-1 digunakan dalam persamaan ke n-2 untuk mendapatkan
nilai x n-2 dan seterusnya.
Jika suatu sistem persamaan tidak berbentuk segitiga,
maka digunakan Operasibaris Elementer (OBE).
4. Operasi Baris Elementer (OBE)
Untuk
menentukan solusi dari Sistem Persamaan Linier dilakukan dengan cara membentuk matrik yang
diperluas/diperbesar dari Sistem Persamaan Linier dan melakukan Operasi Baris Elementer
(OBE) pada matriks yang diperbesar tersebut. OBE ini didapatkan dalam suatu tahapan
dengan menerapkan ketiga tipe operasi berikut untuk menghilangkan bilangan-bilangan
tak diketahui secaras istematik.
- Kalikan persamaan dengan konstanta yang tak sama dengan nol.
- Pertukarkan dua persamaan tersebut.
- Tambahkan kelipatan dari satu persamaan bagi yang lainnya.
Karena
baris (garishorisontal) dalam matriks yang diperbesar beresuaian denganpersamaan
dalam sistem yang diasosiasikan dengan baris tersebut, maka ketiga operasi ini bersesuaian
dengan operasi berikut pada barismatriks yang diperbesar.
- Kalikanlah sebuah baris dengan sebuah konstanta yang tak sama dengan nol.
- Pertukarkanlah dua baris tersebut.
- Tambahkanlah perkalian dari satu baris pada baris yang lainnya.
Operasi-operasi ini dinamakan Operasi
Baris Elementer (OBE).
Contoh dari OBE ini ialah :
x + y + 2z = 9
2x + 4y – 3z = 1
3x + 6y – 5z = 0
Penyelesaian
:
Ubah persamaan tersebut kedalam bentuk
matriks yang diperbesar
Kemudian gunakan OBE :
- Baris kedua : B2 + (-2)B1,
Baris ketiga : B3 + (-3)B1,
- Baris kedua : B2 x (1/2),
3 3. Baris
ketiga : B3 + (-3)B2,
- Baris ketiga : B3 x 2,
B.
Bentuk
Eselon Baris dan Eseolon Baris Tereduksi
Matriks
dapat dikatakan Eselon-baris apabila memenuhi persyaratan berikut :
- Di setiap baris, angka pertama selain 0 harus 1 (leading 1).
- Jika ada baris yang semua elemennya nol, maka harus dikelompokkan di baris akhir dari matriks.
- Jika ada baris yang leading 1 maka leading 1 di bawahnya, angka 1-nya harus berada lebih kanan dari leading 1 di atasnya.
- Jika kolom yang memiliki leading 1 angka selain 1 adalah nol maka matriks tersebut disebutEselon-baristereduksi
Contoh:
- syarat 1: baris pertama disebut dengan leading 1
- syarat 2: baris ke-3 dan ke-4 memenuhi syarat 2
- syarat 3: baris pertama dan ke-2 memenuhi syarat 3
- syarat 4: matriks dibawah ini memenuhi syarat ke-4 dan disebut Eselon-baris tereduksi
OperasiEliminasi Gauss
Eliminasi
Gauss adalah
suatu cara mengoperasikan nilai-nilai di dalam matriks sehingga menjadi matriks
yang lebih sederhana (ditemukan oleh Carl Friedrich Gauss). Caranya adalah dengan
melakukan operasi baris sehingga matriks tersebut menjadi matriks yang Eselon-baris.
Ini dapat digunakan sebagai salah satu metode penyelesaian persamaan linear dengan
menggunakan matriks. Caranya dengan mengubah persamaan linear tersebut ke dalam
matriks teraugmentasi dan mengoperasikannya. Setelah menjadi matriks Eselon-baris,
lakukan substitusi balik untuk mendapatkan nilai dari variabel-variabel tersebut.
Contoh:
Diketahui persamaan linear
Tentukan
Nilai x, y dan z
Jawab:
Bentuk persamaan tersebut ke dalam matriks:
Operasikan
Matriks tersebut
Kemudian
lakukan substitusi balik maka didapatkan:
Operasi Eliminasi Gauss-Jordan
Eliminasi
Gauss-Jordan adalah pengembangan dari eliminasi Gauss yang hasilnya lebih sederhana.
Caranya adalah dengan meneruskan operasi baris dari eliminasi Gauss sehingga menghasilkan
matriks yang Eselon-baris tereduksi. Ini juga dapat digunakan sebagai salah
satu metode penyelesaian persamaan linear dengan menggunakan matriks. Caranya dengan
mengubah persamaan linear tersebut kedalam matriks teraugmentasi dan mengoperasikannya.
Setelah menjadi matriks Eselon-baristereduksi, maka langsung dapat ditentukan
nilai dari variabel-variabelnya tanpa substitusi balik.
Contoh:
Diketahui persamaan linear
Tentukan
Nilai x, y dan z
Jawab:
Bentuk persamaan tersebut kedalam matriks:
Operasikan
Matriks tersebut
BAB 3
PENUTUP
A.
Kesimpulan
1. Sistem Persamaan Linier
Suatu
persamaan linier dalam n peubah (variabel) adalah persamaan dengan bentuk:
a1x1
+ a2x2 + . . . anxn = b
dimana a1, a2 . . . andan b adalah bilangan-bilangan
real dan x1, x2 .
. . x adalah peubah. Dengan demikian maka suatu sistem linier dari m persamaan dalam
n peubah adalah suatu sistem yang berbentuk :
a11x1+
a12x2 + . . . anxn= b1
a21x1+ a2x2
+ . . . a2nxn = b2
.
.
am1x1 + am2x2
+ . . . amnxn =bm
dimana aijdan bi semuanya adalah bilangan
real. Kita akan meyenbut sistem-sistem bentuk 1 sebagai sistem linier m x n
2. Sistem
Ekivalen
tiga
operasi yang dapat digunakan pada suatu sistem untuk memperoleh sistem yang
ekivalen :
a. Urutan
penulisan dua persamaan dapat dipertukarkan
b. Kedua
ruas dari suatu persamaan dapat dikalikan dengan bilangan real bukan nol yang
sama.
c. Kelipatan
dari suatu persamaan dapat dijumlahkan pada persamaan yang lain.
3.
Sistem n x n
Suatu sistem dikatakan memiliki
bentuk segitiga, jika koefisien-koefisien dari k-1 peubah yang pertama dalam persamaan
ke- k semuanya nol dan koefisien dari xk adalah bukan nol (k
=1, …,n).
4.
Operasi Baris Elementer (OBE)
Untuk
menentukan solusi dari Sistem Persamaan Linier dilakukan dengan cara membentuk matrik yang
diperluas/diperbesar dari Sistem Persamaan Linier dan melakukan Operasi Baris Elementer
(OBE) pada matriks yang diperbesar tersebut. OBE ini didapatkan dalam suatu tahapan
dengan menerapkan ketiga tipe operasi berikut untuk menghilangkan bilangan-bilangan
tak diketahui secaras istematik.
5.
Bentuk Eselon Baris dan Eselon Baris
Tereduksi
Matriks
dapat dikatakan Eselon-baris apabila memenuhi persyaratan berikut :
- Di setiap baris, angka pertama selain 0 harus 1 (leading 1).
- Jika ada baris yang semua elemennya nol, maka harus dikelompokkan di baris akhir dari matriks.
- Jika ada baris yang leading 1 maka leading 1 di bawahnya, angka 1-nya harus berada lebih kanan dari leading 1 di atasnya.
- Jika kolom yang memiliki leading 1 angka selain 1 adalah nol maka matriks tersebut disebutEselon-baristereduksi
B.
Saran
Menurut
kami sebagai penulis makalah, makalah ini masih sangat jauh dari kata sempurna.
Masih terdapat banyak kekurangan dalam segi materi ataupun penulisan maka dari
itu kami meminta kritiknya sekaligus saran yang baik bagi makalah kami dari
pihak pembaca. Terima kasih
Soal
Matriks dan sistem persamaan
 Reviewed by Unknown
on
08.53
Rating:
Reviewed by Unknown
on
08.53
Rating:
 Reviewed by Unknown
on
08.53
Rating:
Reviewed by Unknown
on
08.53
Rating:
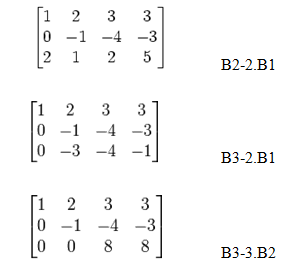


















Soalnya mana?
BalasHapussoal nya baru 2 yg mau jawab silahkan ya:-*
HapusDmana soalnya?
BalasHapus